※一部の数式は長すぎて表示できません。画像をスクロールしてください。
一次方程式の一般形は次のようになります。
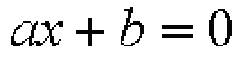
 この方程式の解の公式は次のようになります。
この方程式の解の公式は次のようになります。
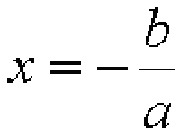 一次方程式の解の公式について、以下のリンク先のページで説明しています。
一次方程式の解の公式について、以下のリンク先のページで説明しています。
二次方程式の一般形は次のようになります。
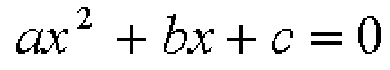
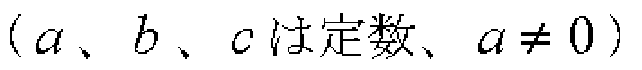 この方程式の解の公式は次のようになります。
この方程式の解の公式は次のようになります。
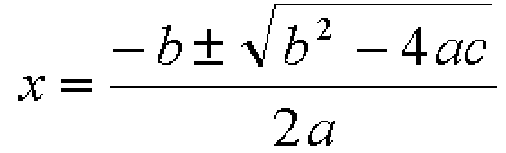 一次方程式の解の公式について、以下のリンク先のページで説明しています。
一次方程式の解の公式について、以下のリンク先のページで説明しています。
三次方程式の一般形は次のようになります。
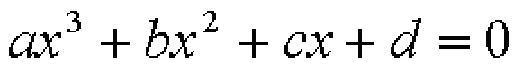
 この方程式の解の公式は次のようになります。
この方程式の解の公式は次のようになります。
 ただし、根号は複素数の範囲で考えて該当する平方根・立方根のいずれか一つを表し、
同じ表記のものは同じ数を表すものとします。また、式中の二つの立方根は次の条件を満たすようにとります。
ただし、根号は複素数の範囲で考えて該当する平方根・立方根のいずれか一つを表し、
同じ表記のものは同じ数を表すものとします。また、式中の二つの立方根は次の条件を満たすようにとります。
 また、(p,q)は下の三組のうちいずれかの値です。
どれをとるかによって三個(重解は重複度の分数える)の解が得られます。
また、(p,q)は下の三組のうちいずれかの値です。
どれをとるかによって三個(重解は重複度の分数える)の解が得られます。
 ここで、ω、ω2は1の立方根のうち虚数のもので(逆でも可)、
ここで、ω、ω2は1の立方根のうち虚数のもので(逆でも可)、
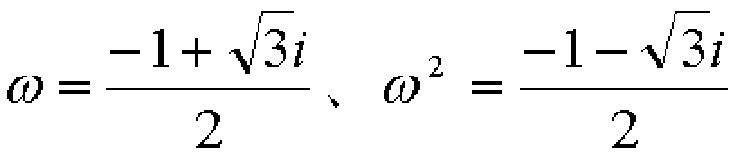 三次方程式の解の公式について、以下のリンク先のページで説明しています。
三次方程式の解の公式について、以下のリンク先のページで説明しています。
四次方程式の一般形は次のようになります。
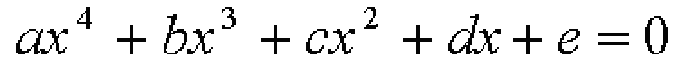
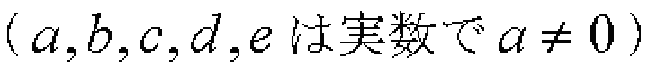 この方程式の解の公式は次のようになります。
この方程式の解の公式は次のようになります。
 新たな文字を置かずに一行に書くとこのうようになってしまいます。
新たな文字を置かずに一行に書くとこのうようになってしまいます。
 ただし書き、記号の説明は省略しました。
四次方程式の解の公式について、以下のリンク先のページで説明しています。
ただし書き、記号の説明は省略しました。
四次方程式の解の公式について、以下のリンク先のページで説明しています。