4次方程式の解の公式

※一部の数式は長すぎて表示できません。画像をスクロールしてください。
四次方程式の一般形は次のようになります。

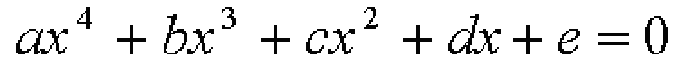
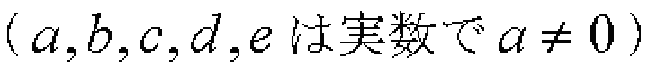まず、四次の係数aで割って次のような形の方程式にします。

…（１）次の関係式でyを定めます。

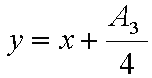…（２）この関係式をxについて解いて、xの方程式に代入することにより、次のような（３次の項が消去された）yの方程式を得ます。

…（３）左辺の一次の項、定数項を右辺に移項した後、両辺にty²を加えて平方完成すると、次のようになります。

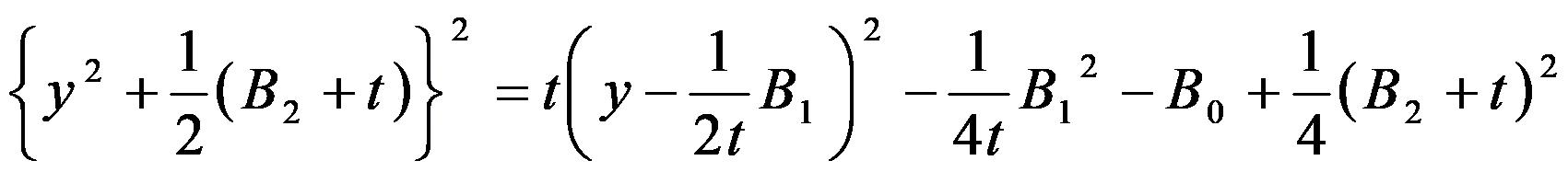…（４）この剰余項＝0という方程式を立てます。

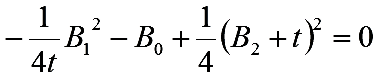…（５）これを整理するとtの三次方程式が得られます。

…（６）この三次方程式を解きます（三次方程式の解の公式参照）。解をt=t₁,t₂,t₃とします（解に0が含まれる場合については PDF参照）。（４）より、

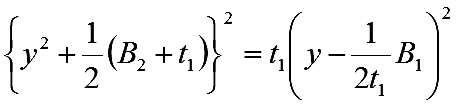…（７）両辺の平方根をとって整理すると、yの二次方程式が二個得られます。

…（８）この２個の二次方程式を解くと、解が合計４個得られます。

…（９）（２）より、xの値が４個得られます。

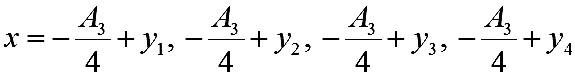…（10）これが最初の四次方程式の解です。もとの係数a,b,c,d,eだけで表したものを1行に書くと次のようになります（とても長い）。ただし書きなどは省略しました。

…（11）四次方程式の解の公式について、以下のPDFで説明しています。

四次方程式の解の公式